La curva de KochFabiana Giacinti, Creación realizada con GeoGebra Se propone su construcción, para ello se guiará con los primeros pasos:
http://personales.unican.es/alvareze |
A través de APLICACIONES con los números, figuras y resoluciones de problemas y de ideas se logra el primer acercamiento para conocer las matemáticas; y mejorar nuestra capacidad para pensarlas con creatividad y lógica. A través de diferentes publicaciones encontrará un camino hacia ellas.
17 de junio de 2012
Geogebra aplicaciones
Los fractales
¿Que es un fractal?

Un fractal es un objeto geométrico en el que se repite el mismo patrón a diferentes escalas y con diferente orientación.
FRACTALES EN LA VIDA COTIDIANA.
Continuamente en nuestras vidas nos encontramos con fractales sin darle la menor importancia. Algunos ejemplos son:


UTILIDAD DE LOS FRACTALES
A continuación se detalla diferentes aplicaciones del estudio de la teoría fractal en una gran variedad de áreas y sus ventajas.
- Cardiologia: Estudia la variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa.
- Geologia: Las técnicas de análisis fractal ayudan a entender las redes de fracturas de los macizos rocosos y las microestructuras de los minerales.
- Fisica. Recientemente se han descubierto una familia de fractales con características similares a las de los spin magnéticos en las transiciones de fase o de los bloques elementales fracturados para los modelos de percolación.Existen modelos estadísticos de Geometría fractal para el análisis de resistencias en estructuras complejas, o de propagación de la corrosión o también para estudiar el comportamiento de aeronaves frente a turbulencias formadas por fuertes ráfagas variables de viento.
- Industria. Durante el zincado o galvanizado de superficies, se produce una distribución idéntica al crecimiento de los corales marinos, con una dimensión fractal del orden de 1,7
- Naturaleza. Los perfiles y grietas de un macizo montañoso presentan autosemejanza fractal, igual que un bosque de helechos o el delta de un gran río. Se ha comprobado que la propagación de un incendio forestal en una plantación ordenada de árboles sigue una conducta fractal.
- Militar. La Geometría fractal ha demostrado su utilidad en la detección de almacenamientos bajo el agua o en la trazabilidad del movimiento de submarinos, como en análisis medioambiental para la determinación del origen y ruta seguida por nubes de lluvia ácida.
- Arte. Al Ampliar los bordes del Conjunto de Mandelbrot se encontra figuras iguales a los mandalas o dibujos budistas introductorios a la meditación. Igualmente se encuentran en las artes islámicas, celtas, egipcias o aztecas. En la pintura abstracta se encuentra obras de Dalí, Escher o Pollock con auténticos diseños fractales. En los sonidos y en la música podemos encontrar distribuciones de frecuencias fractales, desde el ruido de una catarata o el golpeteo de las olas del mar al canto de un pájaro o a una obra de Bach (o de los Beatles). En Arquitectura se puede observar la Sagrada Familia de Gaudí, o los detalles filigranísticos del barroco como verdaderos fractales. Las catedrales góticas son buenos ejemplos de visión intuitiva fractal.
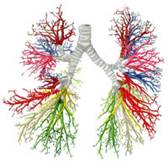
- Nuestro cuerpo. Nuestros pulmones, el sistema sanguíneo, el cerebro, tienen estructuras fractales. Se ajustan a la propiedad de autosemejanza en los cambios de escala. Los pulmones con una superficie cerrada poseen curvas de longitud infinita con grandes grupos de perfiles curvos con exactamente los mismos límites. Así es como maximizan los pulmones su superficie de intercambio. Por ejemplo, los bronquios en sus siete primeras ramificaciones tienen una dimensión fractal diferente a la dimensión de las ramificaciones de mayor nivel. Recuerde que la superficie pulmonar puede cubrir una pista de tenis, mientras que su volumen casi cabe en una pelota de tenis.

CONSTRUCCIONES DE FRACTALES CON GEOGEBRA.
Algunos fractales sencillos como: Triángulo de Sierpinski,
Alfombra de Sierpinski,
La Curva de Koch,
La isla de Koch
Fractal pentagonal.
(próximamente paso a paso para las construcciones con geogebra)
Suscribirse a:
Entradas (Atom)
